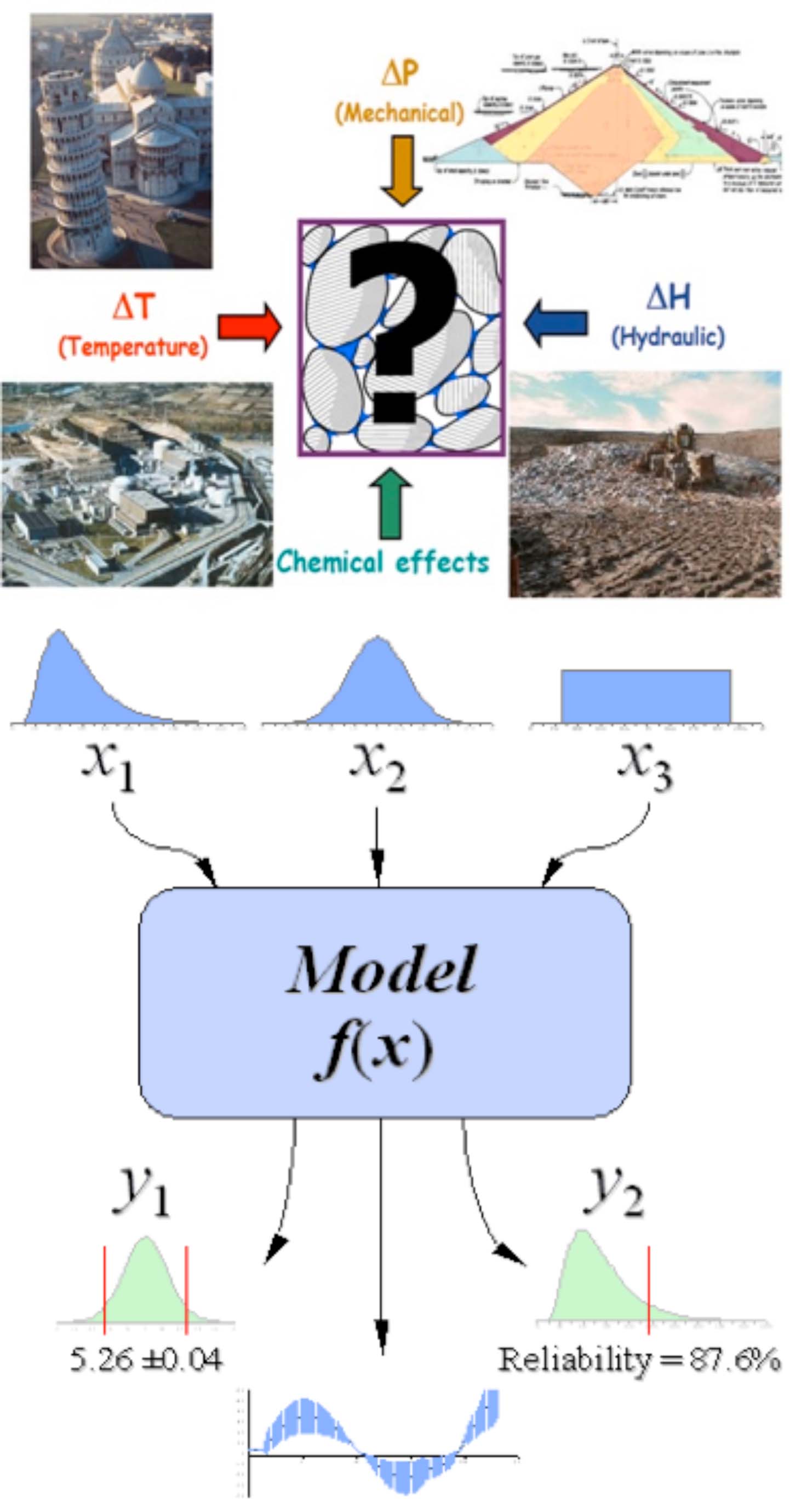
Uncertainty Quantification
 Activitties:
Activitties:
Assessing the effects of the uncertainty from the petrophysical properties of an oil reservoir and field is still a great computational challenge. In this project we will study advanced techniques that, with the help of high performance computation, allow uncertainty propagation (UP) and even optimization under uncertainty studies to be completed in times compatible with the reservoir management practice.
The petrophysical properties of reservoirs will be treated as stochastic fields, with known statistical properties. Reservoir simulation then becomes a non-deterministic problem, whose output must now be stated in terms of statistical moments. Uncertainty propagation is then the problem of finding these moments. One of the most important characteristics of the approaches used in this project is that only non-intrusive techniques will be considered, which in turn, can be implemented with the aid of off-the-shelf commercial simulators, and in particular, the CMG reservoir simulators.
In the first two years of this project, the main research activities will be:
- Karhunen-Love Expansion of stochastic fields
The main input for an UP analysis in reservoir simulation are stochastic fields of permeability and porosity. To represent these fields in terms of a finite number of parameters, which is essential for the solution of the UP problem in terms of solutions of deterministic simulations, we will use the Karhunen-Love Expansion (KLE). In the KLE, an stochastic field is described as a series on the eigenvalues and eigenvectors of its covariance matrix, multiplied by standard random normal variables. The geostatistical characterization of reservoirs can provide equally probable realizations of these stochastic fields, and it is possible to compute numerically an approximation of the covariance matrix of the stochastic field using these realizations. Computing the eigenpairs of the covariance matrix can easily be an intractable problem, since it is a full square matrix with the dimension of the number of cells in the reservoir (for an scalar field). We will implement the Kernel Karhunen-Love Expansion (KKLE), where the eigenpairs of the Kernel matrix are used to compute indirectly, but without any approximation, the eigenpairs of the covariance matrix, and subsequently, the KLE. The dimension of the kernel matrix is equal to the number of the realizations used to compute the covariance matrix, and in general is much smaller than the dimension of the covariance matrix. - Uncertainty propagation with the KLE expansion
An easy, but impractical for realistic problems, technique for UP when the input fields are described by a KLE is simply to apply the Monte Carlo method on the standard normal variables of the KLE. A random number from the standard normal distribution is generated and used as the coefficient of each term of KLE, a sample field is generated from this series, and the field is used as an input to a deterministic reservoir simulation, done with a commercial black box simulator, and the outputs of interest of the simulator are collected for further statistical analysis. This process is repeated until convergence of the statistical moments of interest is achieved, and sample statistics are computed trivially from the collected outputs. The Monte Carlo method is not viable for large scale problems, however, because it demands too many samples to achieve convergence, and in this case each sample implies a full deterministic simulator run that can take many hours. We will still implement this technique, however, because it will be used to assess the accuracy of the more advanced techniques for UP to be implemented later on, that require much fewer simulator runs. - Uncertainty propagation and polynomial chaos methods
As the input of the stochastic simulation problem is described in terms of standard random normal variables when the KLE is used, a natural idea is to approximate the stochastic output as a polynomial on these random variables. This is the main idea behind the polynomial chaos method. This simple idea has deep mathematical foundations, and can be proven to converge under some assumptions. In particular, the statistical moments of the chaos polynomial converge to the statistical moments of the output, but can be computed very cheaply. The most important characteristic of the polynomial chaos method is that it should require many fewer deterministic simulator runs to achieve equivalent accuracy in the computation of moments than the Monte Carlo method. We will implement the polynomial chaos method and test several different techniques to compute the coefficients of the polynomial.
< back >